Recent Works
We develop matrix factorisation methods for pattern set mining in rank data, i.e., data consists of ranking of items, and apply those methods in discovering cancer subtypes and subtype specific features simultaneously.
Rank Matrix Factorisation (RMF) for pattern set mining in rank data
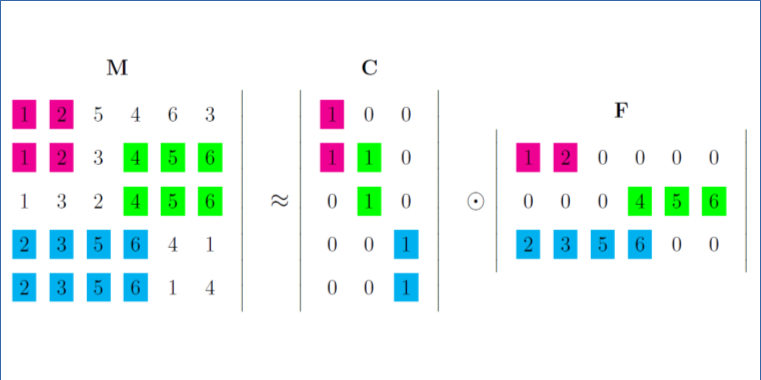
We introduce a generic rank matrix factorisation framework based on semiring theory for pattern set mining in rank data. In this type of data, each row is a complete or partial ranking of the columns.
We succesfully apply the RMF framework for discovering different types of patterns in rank matrices, e.g., Sparse RMF and and ranked tiling, and for cancer subtyping.
References: Le Van et al., Semiring rank matrix factorisation; Le Van et al., Rank matrix factorisation, PAKDD (2015).
Publications
1. Semiring rank matrix factorisation
Thanh Le Van, Siegfried Nijssen, Matthijs van Leeuwen and Luc De Raedt
Journal article IEEE Transactions on Knowledge and Data Engineering, DOI: 10.1109/TKDE.2017.2688374.
Abstract Bibtex2. Simultaneous discovery of cancer subtypes and subtype features by molecular data integration
Thanh Le Van, Matthijs van Leeuwen, Ana Carolina Fierro, Dries De Maeyer, Jimmy Van den Eynden, Lieven Verbeke, Luc De Raedt, Kathleen Marchal, and Siegfried Nijssen
Journal article Bioinformatics (2016) 32 (17): i445-i454 doi:10.1093/bioinformatics/btw434
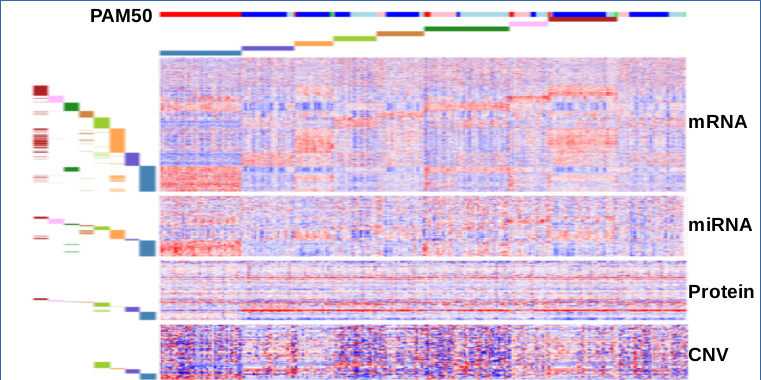
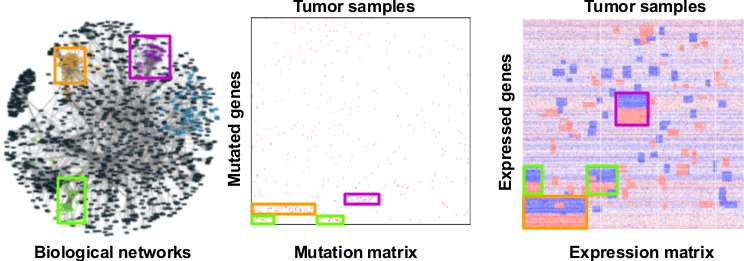
Abstract Bibtex Pdf CodeSubtyping cancer is key to an improved and more personalized prognosis/treatment. The increasing availability of tumor related molecular data provides the opportunity to identify molecular subtypes in a data-driven way. Molecular subtypes are defined as groups of samples that have a similar molecular mechanism at the origin of the carcinogenesis. The molecular mechanisms are reflected by subtype-specific mutational and expression features.
Data-driven subtyping is a complex problem as subtyping and identifying the molecular mechanisms that drive carcinogenesis are confounded problems. Many current integrative subtyping methods use global mutational and/or expression tumor profiles to group tumor samples in subtypes but do not explicitly extract the subtype-specific features. We therefore present a method that solves both tasks of subtyping and identification of subtype-specific features simultaneously. Hereto our method integrates mutational and expression data while taking into account the clonal properties of carcinogenesis. Key to our method is a formalisation of the problem as a \emph{rank matrix factorisation} of \emph{ranked data} that approaches the subtyping problem as \emph{multi-view bi-clustering}.
3. Rank matrix factorisation
Thanh Le Van, Matthijs van Leeuwen, Siegfried Nijssen and Luc De Raedt
Conference paper The 19th Pacific-Asia conference on knowledge discovery and data mining (PAKDD 2015). HoChiMinh City, VietNam, 19-22 May 2015 (pp. 734-746) Springer.
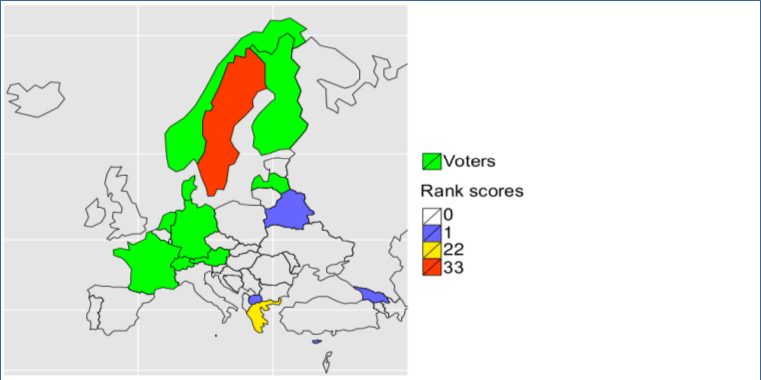
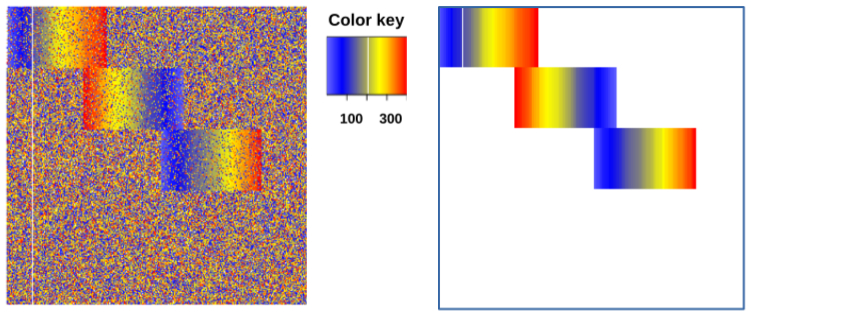
Abstract Bibtex Pdf CodeWe introduce the problem of \emph{rank matrix factorisation} (RMF). That is, we consider the decomposition of a rank matrix, in which each row is a (partial or complete) ranking of all columns. Rank matrices naturally appear in many applications of interest, such as sports competitions. Summarising such a rank matrix by two smaller matrices, in which one contains partial rankings that can be interpreted as local patterns, is therefore an important problem.
After introducing the general problem, we consider a specific instance called Sparse RMF, in which we enforce the rank profiles to be sparse, i.e., to contain many zeroes. We propose a greedy algorithm for this problem based on integer linear programming. Experiments on both synthetic and real data demonstrate the potential of rank matrix factorisation.
4. Ranked tiling
Thanh Le Van, Matthijs van Leeuwen, Siegfried Nijssen,Ana Carolina Fierro, Kathleen Marchal and Luc De Raedt
Conference paper The European Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases 2014 (ECML/PKDD 2014), Nancy, France, 15-19 September 2014, (pp. 98-113) Springer.
Abstract Bibtex Pdf CodeTiling is a well-known pattern mining technique. Traditionally, it discovers large areas of ones in binary databases or matrices, where an area is defined by a set of rows and a set of columns. %However, it cannot be applied on data that is not binary. In this paper, we introduce the novel problem of {\em ranked} tiling, which is concerned with finding interesting areas in ranked data. In this data, each transaction defines a complete ranking of the columns. Ranked data occurs naturally in applications like sports or other competitions. It is also a useful abstraction when dealing with numeric data in which the rows are incomparable.% due do incompatible scales.
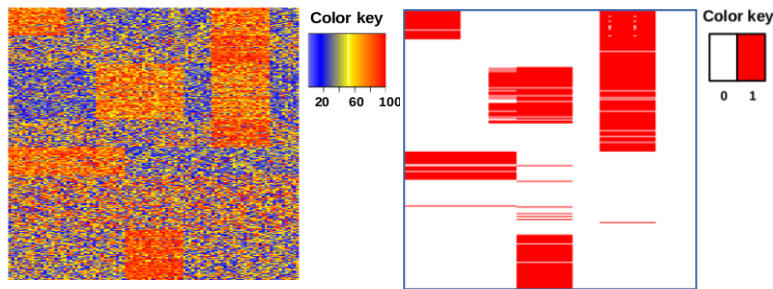
We introduce a scoring function for ranked tiling, as well as an algorithm using constraint programming and optimization principles. We empirically evaluate the approach on both synthetic and real-life datasets, and demonstrate the applicability of the framework in several case studies. One case study involves a heterogeneous dataset concerning the discovery of biomarkers for different subtypes of breast cancer patients. An analysis of the tiles by a domain expert shows that our approach can lead to the discovery of novel insights.
5. Mining local staircase patterns from noisy data
Thanh Le Van, Ana Carolina Fierro, Tias Guns, Matthijs van Leeuwen, Siegfried Nijssen, Luc De Raedt and Kathleen Marchal
Workshop paper International workshop on Co-Clustering and Applications (CoClus'12) in conjunction with IEEE ICDM 2012. Brussels, 10 December 2012 (pp. 139-146) IEEE Computer Society.
Abstract Bibtex Pdf CodeMost traditional biclustering algorithms identify biclusters with no or little overlap. In this paper, we introduce the problem of identifying staircases of biclusters. Such staircases may be indicative for causal relationships between columns and can not easily be identified by existing biclustering algorithms. Our formalization relies on a scoring function based on the Minimum Description Length principle. Furthermore, we propose a first algorithm for identifying staircase biclusters, based on a combination of local search and constraint programming. Experiments show that the approach is promising.
6. Deriving financial aid optimization models from admissions data
Thanh Le Van and Peter Haddawy
Conference paper 37th Annual Frontiers In Education Conference - Global Engineering: Knowledge Without Borders, Opportunities Without Passports, 2007 (pp. F2A-7-F2A-12), IEEE Computer Society.
Abstract Bibtex PdfThis paper presents a novel approach to deriving probabilistic models that predict enrollment given applicant background and the amount of financial aid offered. Our Bayesian network models can be used to optimize various enrollment objectives. We present a novel efficient optimization algorithm that uses the models to maximize expected tuition revenue under capacity constraints including student-faculty ratio and accommodation. We demonstrate and evaluate our approach using four years of graduate admissions data from the Asian Institute of Technology, consisting of 7,788 applicants from 84 different countries. This data set is particularly challenging since reliable family income data is not available for students from most of these countries. Evaluating the Bayesian network model with 10-fold cross validation yields an ROC Az value of 0.8451, with a predictive accuracy of 82.70% at a threshold of 0.5. Comparing the results of the tuition revenue optimization model to the institute's current financial aid allocation practice shows that if single-term tuition revenue is the sole optimization criterion, the institute can achieve its current enrollment numbers while realizing significant savings in its financial aid budget. The prediction and optimization software is currently being incorporated into the institute's online admissions processing system.
Software
Ranked tiling.
Ranked tiling discovers a set of ranked tiles, which are data regions having high ranks, in rank matrices. There are two models for ranked tiling. The first model uses Constraint Programming (CP) and the model developed later uses Semiring Rank Matrix Factorisation. They are both implemented in Scala using OscaR library. The CP implementation uses OscaR CP solver and the other implementation has Gurobi as the back-end solver.
Coming soonSparse RMF.
Sparse RMF finds a set of partial rankings repeatedly occurring in a rank matrix. Such sets of partial rankings can be used to succinctly summarise the given rank matrix and show the main categories of the rankings. Sparse RMF is implemented in Scala. It uses OscaR library to write the optimisation model for Sparse RMF, which are Integer Linear Programs, and uses Gurobi as the back-end solver.
SourcecodeSRF - Subtyping through Ranked Factors.
SRF integrates Boolean mutation data, numeric gene expression data (microarray or RNASeq), and prior knowledge encoded in biological networks to discover cancer subtypes and subtypes features. SRF is implemented in Scala using OscaR library and Gurobi solver.
GithubContact
MAGNET group
INRIA in Lille - France
thanh.le-van@inria.fr
thanhlv@gmail.com
+33769094168